Go is a game in which two opponents vie for domination of a playing space. Also known as Wei Qi (China), Igo (Japan), and Baduk (Korea), it is quite possibly the oldest board game in the world. Go has been played for literally thousands years since its invention in China.
Go is an excellent example of how complexity arises from simplicity. Though a typical game is so complicated that no current Go program can beat a professional human (unlike chess), the basic game can be completely described by a short list of rules, with some terms explained below:
- Equipment The playing space is a square grid of agreed size with an odd number of lines. Each player has a collection of colored stones; one player’s stones are Black, the other’s White.
- Moves Beginning with the player of Black stones, players alternate moves. Each move consists of either a) a pass, in which the player does nothing, or b) placing a stone of one’s own color on an empty intersection of the grid and removing any dead stones that result (opponent stones first).
- Ending The game ends when both opponents agree further play is useless, either because they are repeating a cycle of moves or because both players pass.
- Scoring The game is tied if the opponents end because of a repeating cycle. If the game is played out until both opponents pass, the player with the greater number of stones and eyes on the grid wins.
That’s all—though we need to define the terms in bold above. The definitions both apply to the concept of a stone’s life or death.
To see why this distinction is so crucial, imagine an early version of Go in which the rules are the same except that no stones are removed from the grid. The goal is still to dominate the space by having the most stones on it—but now the Black player is guaranteed to win. On a 7 x 7 grid, for example, Black (by virtue of moving first) will be able to place 25 stones to White’s 24. Not much of a game.
There must then be some mechanism for removing stones from the board, so that White has a chance to catch up to Black. Once the concept of a stone’s life or death is established, we can decree that dead stones are removed from the space. The result is a dynamic, unpredictable game.
So what is life and death for a stone? Figure 1 shows the first move of a Go game. The Black stone occupies an intersection of the grid (a point), and the grid lines connect that point to four other points—those adjacent vertically and horizontally. Notice that, according to the rules, stones never move from one place to another on the board. But the grid lines do define which points are connected.
If a stone is connected by a grid line to an adjacent stone of its color, those stones form a group. In fact, any number of stones can form a group—as long as adjacent stones all connect to each other by grid lines. Figure 2 shows some examples of groups, two White and two Black.
Diagonal stones are NOT connected. Figure 3 shows unconnected stones that do not form a united group, since no stone connects to an adjacent stone by a grid line. (Technically, each stone forms a “group” of one stone.) Make sure you understand which patterns form single groups!
Now we can define life and death: Any group of stones (even a group of one stone) is alive if at least one stone in the group connects to an empty point. (Such points are called liberties.)
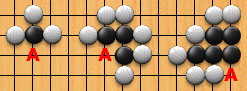
This means it is possible to kill a group of enemy stones by filling its adjacent points with one’s own stones. Figure 4 depicts Black groups that will die when White places a stone on the point marked A:
…and since dead stones are removed, Figure 5 shows how those same positions will appear after White’s turn is over:
Note that it is possible to commit suicide! In Figure 6, White can kill his entire group by playing at A. (It’s hard to imagine why he’d want to.)
This leads to an interesting question: Can Black kill the White group in Figure 7? It looks like suicide, but the rules specify that dead opponent stones are removed before dead stones of one’s own. So Black can play at A, after which the dead White stones are removed. The result is in Figure 8. Since the piece Black played at A is no longer surrounded, it is not dead and remains on the board.
Already, we’ve seen some complexity developing from the simple rules. But there’s one more important quirk that arises: Some groups can achieve immortality.
Recall that in Figure 7, Black was able to play on a point with no liberties inside a White group, because doing so removed White’s last liberty and killed the White stones. But look at Figure 9, in which a White group completely encloses two points. You might think Black could kill this group, too—but it’s impossible.
If Black plays in the top enclosed point, White still has a liberty at bottom; the Black stone is only committing suicide. Likewise, if Black plays in the bottom enclosed point, White still lives because of the liberty at top; again, the Black piece is removed. Since Black can never fill both liberties on one turn, the White group will always have at least one liberty. By definition, the White group is always alive. It is immortal.
Note that a group must separately enclose the two liberties to become immortal. The opponent can play on liberties that aren’t enclosed without committing suicide, so external liberties can’t make a group immortal. Watch what happens to the Black group in Figure 10, which has one enclosed liberty and one outside liberty:
First, White fills the outside liberty. Black can move anywhere, perhaps in the corner space as shown above, but that’s not part of the other Black group and is no help. Next, White plays inside the Black group, filling its last liberty. The Black stones are dead, so they are removed. The last diagram shows the end result.
So both liberties must be enclosed. But they also must be separated, or else the opponent can fill one liberty in—as in Figure 11. Although the White stones enclose two liberties, the group is as good as dead. Since the liberties aren’t separated, Black can fill one without committing suicide. Now the White group has only one liberty and can be killed on Black’s next move.
If you’ve been paying attention, you may be looking at the Figure 11 end position and thinking, “But the Black piece has only one liberty itself—and it’s White’s move! Can’t White just kill the Black piece to be safe?” Good question! Let’s see what happens if White tries that.
Figure 12 shows the position after White plays in the empty point, killing (and removing) the Black invader. But by playing inside the enclosure, White has removed one of the liberties. Now it’s Black’s turn again, and the White group has only one liberty. Figure 13 shows the inevitable conclusion. In essence, Black has sacrificed one stone to capture 10 and control that region of the grid.
The two separately enclosed liberties required for immortality are called, unsurprisingly, eyes. Now you have all the information you need to understand the rules… although we’ve only scratched the surface of Go’s complexity. With so much literature available in print and online, I won’t attempt to cover the resulting intricacies. Some links to additional resources are included at the bottom.
But first, a word of warning: The rules as stated above are specifically for what I termed the “basic game” of Go. I intend this in the sense of a Platonic ruleset—the simplest, primal rules from which today’s rulesets are derived. In fact, I doubt any serious Go player anywhere in the world plays by the rules outlined here.
So why formulate the rules this way? Well, for one thing, the rules of Go already vary by country or even player. (The most common rulesets are from Japan or China.) But modern rulesets over the millennia have accumulated rules that are “patches,” designed to eliminate aspects of play that people have found upsetting. Most rules, for example, forbid an endless cycle of moves, which means no game ends in a tie. If you don’t want tied games, by all means play by those rules. But I find the ruleset here the most appealing variation for two reasons: 1) It is the simplest and most elegant formulation of rules and 2) it allows the most scope for player skill.
The rule prohibiting an endless cycle of moves, for example, requires players to remember playing positions and never repeat them. This is neither simple nor elegant. Many rulesets forbid suicide, seeing it as pointless. But why not allow players the option? Finally, a player’s score in some rulesets is based on enemy stones captured as well as grid points controlled. I prefer the purity of vying solely for domination of the grid, but that’s just a personal taste. Whichever ruleset you choose, I hope you enjoy playing.
Endnotes
- For the curious, I’ll add here that these rules are one step simplified from the New Zealand rules (by eliminating the “ko” rule forbidding endless cycles of moves). The NZ rules, in turn, are a simpler formulation of Chinese rules, which evolved into the highly [and needlessly, in my opinion] complex Japanese rules. Unfortunately, many newcomers to Go are introduced to the Japanese rules first and find their arbitrary nature off-putting. If you want to play an internationally recognized ruleset instead of the Platonic rules outlined here, I recommend the Chinese rules.]
- Though the above represent the necessary and sufficient rules to play, some conventions may prove helpful. The standard grid size, for example, is 19 x 19; 13 x 13 and 9 x 9 grids are common, particularly among learners. There’s no avoiding the fact that moving first gives Black a strong advantage, so the best solution is to play an even number of games against the same opponent, alternating colors each game. If that’s not possible, you may want to give White a score adjustment to compensate; often, White is awarded 5.5 points (the ½ point ensures the game isn’t tied).
All figures on this page were created in Goban, by Sen:te.
For further exploration:
- Compendium of Rules for Wei-Qi (Go, Baduk) Comparison of the permutations of Go rulesets.
- John’s Go Page Rules, tutorial, links.
- American Go Association home page.